セーリングヨットなのに、船のサイズに比べて2回りぐらい大きなエンジンを積んで、「うちは機走8ノットですわ」とか自慢しているおじさんに遭遇することがある。
船の最大速力は、ほぼ水線長で決まり、プレーニングしない限りは、速長比、即ち速度(kt)を水線長(ft)の平方根で割った係数で1.34 以上の速度は出せないとされている。自艇に当てはめると水線長が、10m(32.7ft)なので7.6 kt ぐらいになり、これをハルスピードと呼ぶ。「機走8ノットですわ」おじさんの船はどう見ても、うちより小さいからハルスピードはもっと小さいはずなのだが…
一方、うちの船の場合、機関出力70%ぐらいですぐに6.7kt ぐらいになるが、7ktになるともう苦しく、7.6kt(ハルスピード)なんて出ない。その一方、ジェネカーを揚げてフリーを走ったりすると8kt 出ちゃうことだってあるが、どう見てもプレーニングしている様子はない。
これらをずっと不思議に思っていた。
そこで、買っただけでずっと本棚にしまい込まれていた「ヨットデザイン原論」(Larsson & Eliasson 著、大橋且典さん翻訳監修、以下「原論」)を引っ張り出してきて飛ばし読みしていたら面白いことがわかった。

原論では、速長比でなく、より一般化しやすいフルード数という無次元数を使う。速長比は速度を水線長の平方根で除したものだが、フルード数は、速度(m/s)を水線長(m)と重力加速度の積の平方根で除す(Fn = V/(g*L)^(1/2))。
そして、このフルード数が0.40になるとき、ちょうど水線長と船が自分で作る波の波長が同じぐらいになり、非常に大きな抵抗が生じる。この時の速長比が、最初に出て来た1.34だ。
さて、原論78ページには、フルード数と船が受ける抵抗に関してこんなグラフが出ていた。
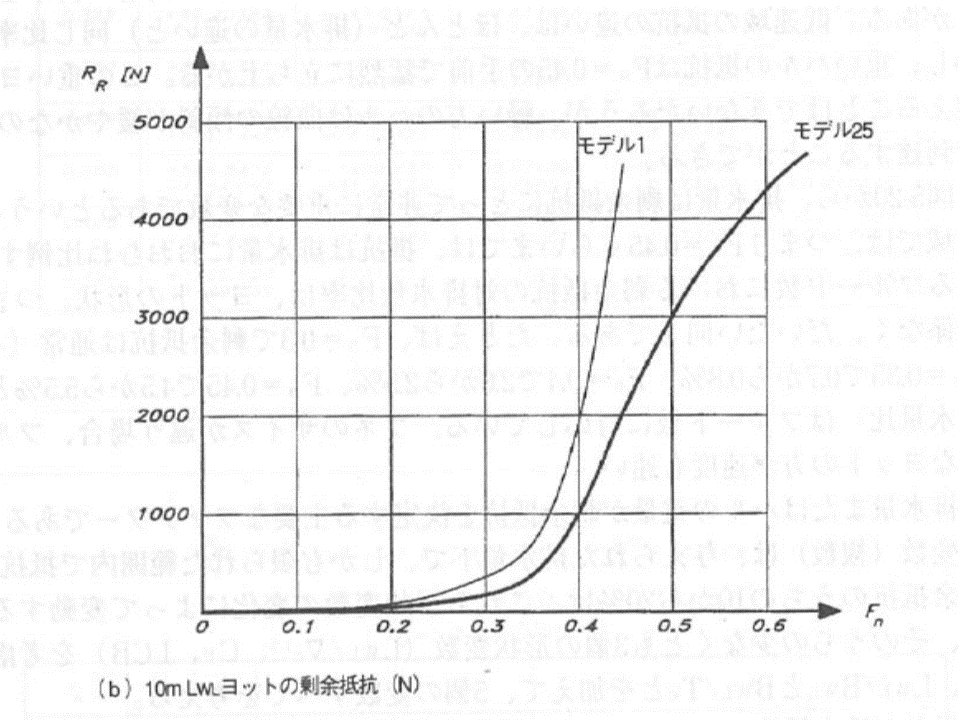
これは船にかかる剰余抵抗(造波抵抗と粘着圧力抵抗の和)を、水線長10mの2種類のボートについてシミュレーションした結果で、モデル1が重排水量艇(9.18トン)、モデル25が、軽排水量のレーサー(4.62トン)を表している(うちは6.5トンなのでちょうどこの中間になる)。
このグラフをみると、Fn=0.33付近に抵抗が急激に増える変節点がある、自艇でいうとFn=0.33はだいたい6.7kt でドンピシャ。また、Fn=0.40付近でいきなり抵抗が増すのではなく、Fn=0.33を超えるとすぐに急カーブで抵抗が増していくので、うちのアンダーパワーなエンジン(28Hp)ではフルード数0.37(スピードにして7.2kt)ぐらいが限界ということなのだろう。
次に、何故プレーニングしないでもハルスピードを超えられるのかということについて、原論の74ページに以下の記述を見つけた。
「抵抗曲線中最大のバンプは、波長が水線長と等しくなった時、つまりFn=0.40のときに起こるはずである。しかし実際にはもう少し高いフルード数のところ、つまりもう少し高いスピードのところで起こる。これはバウとスターンのオーバーハングによって。バウウェーブとスターンウェーブとの間の距離が名目上の水線長より長くなるからである。だから最終バンプは普通はフルード数0.5付近で起こる。」
なるほどそいういう事か。係数1.34は一つの目安だが、通常航走における理論的限界速度(逆にそれを大パワーで乗り切れば滑走に入る)まではもう少し余裕があり、速長比1.34を超えても、まだしばらくパワー次第では通常航走でも速度を伸ばすことができるがまだ滑走には入らないという微妙な速度レンジがあるという事だ。
したがって「機走8ノットですわ」おじさんは決して嘘つきでは無い!まあ、何でモーターボートにしないの?って聞いてみたくなったりするけども。
(2023年9月加筆修正)


コメント